
Các số liệu đánh giá cho mô hình hồi quy khá khác so với các số liệu ở trên mà chúng ta đã thảo luận cho các mô hình phân loại bởi vì chúng tôi hiện đang dự đoán trong một phạm vi liên tục thay vì một số lớp rời rạc. Nếu mô hình hồi quy của bạn dự đoán giá một ngôi nhà là 400 nghìn đô la và nó được bán với giá 405 nghìn đô la thì đó là một dự đoán khá tốt. Tuy nhiên, trong các ví dụ phân loại, chúng tôi chỉ quan tâm đến việc một dự đoán đúng hay sai, không có khả năng nói một dự đoán là "khá tốt". Do đó, chúng tôi có một bộ số liệu đánh giá khác nhau cho các mô hình hồi quy.
Mean Squared Error
Mean Squared Error (MSE) có lẽ là số liệu phổ biến nhất được sử dụng cho các bài toán hồi quy. Về cơ bản, nó tìm thấy sai số bình phương trung bình giữa các giá trị được dự đoán và thực tế. MSE là thước đo chất lượng của một công cụ ước tính - nó luôn không âm và các giá trị càng gần 0 càng tốt.
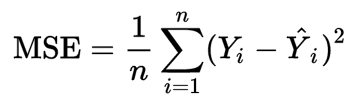
trong đó n là số điểm dữ liệu, yᵢ là giá trị quan sát và ŷ ᵢ là giá trị dự đoán.
Trong phân tích hồi quy, vẽ biểu đồ là một cách tự nhiên hơn để xem xu hướng chung của toàn bộ dữ liệu. Đơn giản MSE cho bạn biết mức độ gần của đường hồi quy với một tập hợp các điểm. Nó thực hiện điều này bằng cách lấy khoảng cách từ các điểm đến đường hồi quy (những khoảng cách này là “sai số”) và bình phương chúng. Bình phương là rất quan trọng để giảm độ phức tạp với các dấu hiệu tiêu cực. Nó cũng tạo ra nhiều trọng lượng hơn cho sự khác biệt lớn hơn.
Để giảm thiểu MSE, mô hình có thể chính xác hơn, có nghĩa là mô hình gần với dữ liệu thực tế hơn. Một ví dụ về hồi quy tuyến tính sử dụng phương pháp này là - phương pháp bình phương nhỏ nhất đánh giá sự phù hợp của mô hình hồi quy tuyến tính với tập dữ liệu hai biến, nhưng giới hạn của nó liên quan đến phân phối dữ liệu đã biết.
MSE càng thấp thì dự báo càng tốt.
Mean Absolute Error
Mean Absolute Error (MAE) đo độ lớn trung bình của các lỗi trong một tập hợp các dự đoán mà không cần xem xét hướng của chúng. Đó là giá trị trung bình trên mẫu thử nghiệm về sự khác biệt tuyệt đối giữa dự đoán và quan sát thực tế, trong đó tất cả các khác biệt riêng lẻ có trọng số bằng nhau.
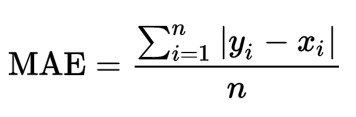
trong đó n là số điểm dữ liệu, xᵢ là giá trị thực và yᵢ là giá trị dự đoán.
Có thể diễn đạt MAE là tổng hòa của hai thành phần: Bất đồng về số lượng và Bất đồng về phân bổ.
MAE được biết đến là mạnh mẽ hơn đối với các yếu tố ngoại lai so với MSE. Lý do chính là trong MSE bằng cách bình phương các sai số, các giá trị ngoại lai (thường có sai số cao hơn các mẫu khác) được chú ý nhiều hơn và chiếm ưu thế trong sai số cuối cùng và tác động đến các tham số của mô hình.
Root Mean Square Error
Root Mean Square Error (RMSE) hoặc Root Mean Square Deviation (RMSD) là căn bậc hai của mức trung bình của các sai số bình phương. RMSE là độ lệch chuẩn của các phần dư (sai số dự đoán).
Phần dư là thước đo khoảng cách từ các điểm dữ liệu đường hồi quy; RMSE là thước đo mức độ dàn trải của những phần dư này, nói cách khác, nó cho bạn biết mức độ tập trung của dữ liệu xung quanh đường phù hợp nhất.
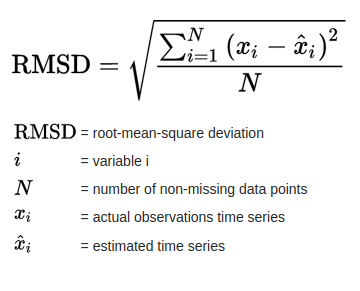
Ảnh hưởng của mỗi lỗi đối với RMSE tỷ lệ với kích thước của lỗi bình phương; do đó các sai số lớn hơn có ảnh hưởng lớn đến RMSE một cách không cân xứng. Do đó, RMSE nhạy cảm với các yếu tố ngoại lai. Sai số bình phương trung bình gốc thường được sử dụng trong khí hậu học, dự báo và phân tích hồi quy để xác minh kết quả thực nghiệm.
Khi các quan sát và dự báo chuẩn hóa được sử dụng làm đầu vào RMSE, có mối quan hệ trực tiếp với hệ số tương quan . Ví dụ, nếu hệ số tương quan là 1, RMSE sẽ bằng 0, bởi vì tất cả các điểm nằm trên đường hồi quy (và do đó không có sai số).
RMSE luôn không âm và giá trị 0 (hầu như không bao giờ đạt được trong thực tế) sẽ chỉ ra sự phù hợp hoàn hảo với dữ liệu. Nói chung, RMSD thấp hơn sẽ tốt hơn RMSD cao hơn.
